CHE COS'È LA MATEMATICA? INTRODUZIONE ELEMENTARE AI SUOI CONCETTI E METODI

DISPONIBILITÀ GARANTITA AL 99%; SPEDIZIONE ENTRO 12 ORE DALL'ORDINE. OTTIME CONDIZIONI GENERALI, MAI SFOGLIATO, SEGNI DEL TEMPO ALLA COPERTINA.

L'opera si presenta come un libro introduttivo alla matematica e ai suoi metodi, che, nelle intenzioni degli autori, intende rivolgersi a una platea molto ampia: studenti universitari e liceali, professori di scuola secondaria, ma anche specialisti della materia, oltre a un pubblico più generale di persone colte e profane, ma con un forte interesse alla matematica. L'impostazione è tale che lettura del libro è accessibile, in generale, a chi possieda un bagaglio di cultura matematica di livello liceale, anche se la penetrazione e la comprensione dei concetti fondamentali esposti nel libro richiede un certo sforzo intellettuale.
Gli argomenti di cui si occupa sono la teoria dei numeri, combinatoria, geometria euclidea, geometria proiettiva, geometrie non euclidee, geometria differenziale, topologia, topologia algebrica, calcolo infinitesimale.
I numeri naturali e la teoria dei numeri
Il sistema dei numeri in matematica: numeri razionali, reali, complessi
Costruzioni geometriche
Geometria proiettiva. Assiomatica. Geometrie non Euclidee
Topologia
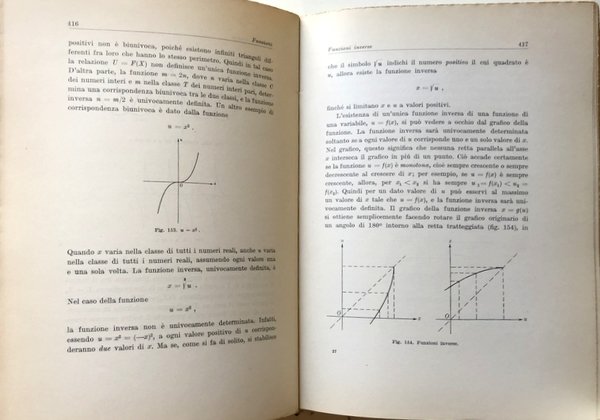
Funzioni e limiti
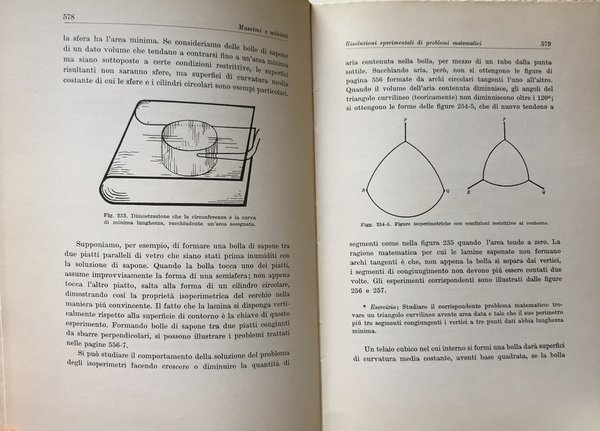
Massimi e minimi
Il calcolo. Derivate e integrali.
Sviluppi recenti
Appendice. Osservazioni, problemi ed esercizi
Secondo il matematico Michael Katehakis, il titolo del libro sarebbe ispirato a Che cos'è l'arte? di Lev Tolstoj: la congettura si basa sulla grande passione di Robbins per la letteratura, e per Tolstoj in particolare, e sul fatto che Robbins ha fatto qualcosa di analogo nel libro Great Expectations: The Theory of Optimal Stopping, scritto insieme a Y. S. Chow e David Siegmund, il cui titolo presenta una chiara assonanza con quello del romanzo Great Expectations di Charles Dickens. In seguito, il titolo del saggio divulgativo ha ispirato la scelta di Reuben Hersh per il suo What Is Mathematics, Really? (Cos'è davvero la matematica?), un saggio di filosofia della matematica.
Concepito per principianti e scienziati, per studenti e insegnanti, per filosofi e ingegneri, il libro offre una illustrazione accessibile del mondo matematico. Scritto in ordine sistematico, il libro può essere letto anche per gruppi di capitoli a seconda delle esigenze conoscitive e didattiche, e in ogni caso l'esposizione gradua sempre opportunamente le difficoltà. In questa nuova edizione, il curatore ha aggiunto commenti e integrazioni in vari luoghi del testo e un intero capitolo dedicato ai recenti sviluppi della matematica.

Descrizione bibliografica
Titolo: Che cos'è la matematica? Introduzione elementare ai suoi concetti e metodi
Titolo originale: What is Mathematics? An Elementary Approach to Ideas and Methods
Autore: Richard Courant, Herbert Robbins
Traduzione di: Prof. Liliana Ragusa Gilli
Editore: Torino: Giulio Einaudi, 1950
Lunghezza: 754 pagine; 24 cm; illustrato
Peso: 1,5 Kg
Collana: Volume XXV 25 di Biblioteca di cultura scientifica
Soggetti: Matematica, Saggi, Classici, Divulgazione scientifica, Scienze matematiche, Didattica, Comprensione, Pedagogia, Filosofia, Storia, Problemi, Numeri Primi, Operazioni, Aritmetica, Geometria, Serie, Gruppi, Variabili, Esercizi, Calcolo differenziale, Metodo, Metodi numerici, Teorie, Teoremi, Fermat, Matematica divulgativa seria, Oxford University Press, 1941, Albert Einstein, Albero di Steiner, Ian Stewart, Congettura di Goldbach, Dimensione di Hausdorff, Frattali, Topologia, Algebra, Eulero, Analisi, Binomi, Progressioni, Funzioni, Equazioni, Integrali, Induzione, Decimali, Libri Vintage, Fuori catalogo, Manuali, Euclidean geometry, Leibniz, Hence, Jordan curve, Cantor, De Moivre, Liouville, Apollonio, Cubo, Cerchio, Assiomatica, Pascal, Desatgues, Brianchon, Poliedri, Wierstrass, Dirichlet, Schwarz, Derivate, Bibliografia, Prime edizioni, Mathematics, Essays, Classics, Scientific Dissemination, Mathematical Sciences, Didactics, Comprehension, Pedagogy, Philosophy, History, Problems, Prime Numbers, Operations, Arithmetic, Geometry, Series, Groups, Variables, Exercises, Differential Calculation, Method, Numerical Methods, Theories, Theorems, Serial popularization, Steiner tree, Conjectures, Dimensions, Fractals, Topology, Analysis, Binomials, Progressions, Functions, Equations, Integrals, Induction, Decimals, Books out of stock/print, Manuals, Apollonius, Cube, Circle, Axiomatics, Polyhedra, Derivatives, Bibliography, First Editions

Parole e frasi comuni
a e b algebrico angoli base bi-rapporto calcolo caso cerchio coefficienti concetto conica continua coordinate corrispondenza costruire costruzione curva dato decimale definita definizione equazione insieme derivata dimensione dimostrazione diseguaglianza distanza divisore elementi equazioni equivalente esempio Esercizio euclidea Eulero Fermat Figura forma formula funzione continua funzione esponenziale funzione f(x generale geometria proiettiva intersecano intersezione intervalli area esistenza espressione integrale ipotesi lati lettore limite lunghezza massimo matematica metodo minimo nastro di Möbius numeri complessi numeri interi numeri interi positivi numeri razionali numeri reali numero positivo parallele piano polinomio principio induzione problema procedimento proiezione proprietà raggio ragionamento risultato segmento semplice serie geometrica simbolo sistema soluzione somma sottoinsieme Steiner successione monotona superfici superficie tangente teorema Bolzano teoria teoria dei numeri topologica trasformazione uguale valore variabile vertici